 |
 |
이번 비디오에서는 확률의 기초 개념을 다룬다.
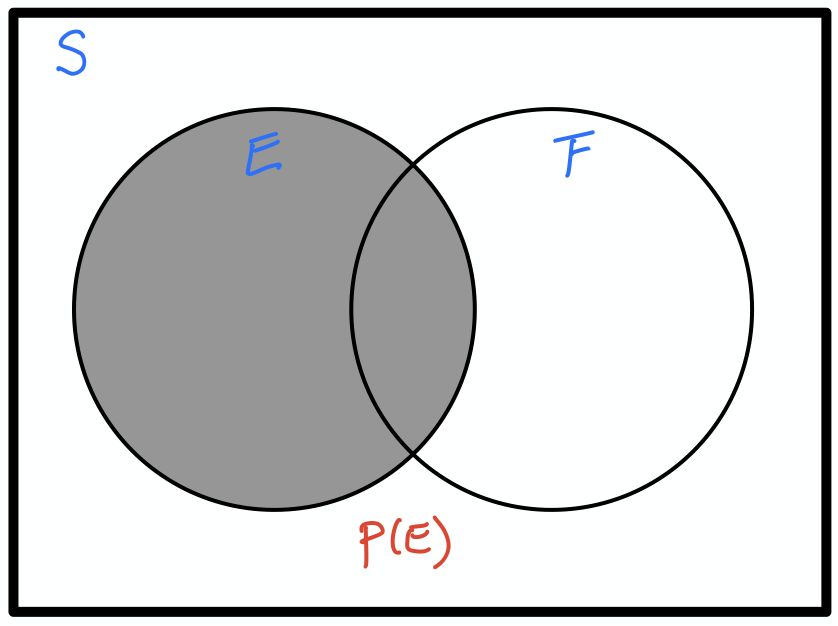
확률(probability)은 특정 사건과 관련된 불확실성을 측정하는 방법이다. 이때 사건은 표본 공간이라 불리는 집합의 부분집합이어야 한다.
예를 들어, 주사위 던지기에서 표본 공간은 1부터 6까지의 정수들의 집합이다. 이 공간의 부분집합들이 모두 사건이 된다. 예를 들어,
등을 모두 주사위 던지기의 사건으로 볼 수 있다. 사건 $E$가 발생할 확류를 $P(E)$로 나타낸다.
앞으로 많은 모델을 만들 것이며, 모델의 성능을 평가하기 위해 확률을 사용한다. 여기서 다루는 주제는 다음과 같다.
두 사건 $E$와 $F$에 대해, 두 사건사이의 관계를 종속과 독립으로 구분할 수 있다.
두 사건 $E$와 $F$가 동시에 발생할 확률을 $P(E, F)$라 하자. 그러면 두 사건 사이의 종속과 독립 관계를 아래와 같이 쉽게 판단할 수 있다.
실제로
$$P(E, F) = \frac 1 4 = \frac 1 2 \cdot \frac 1 2 = P(E) \cdot P(F)$$실제로
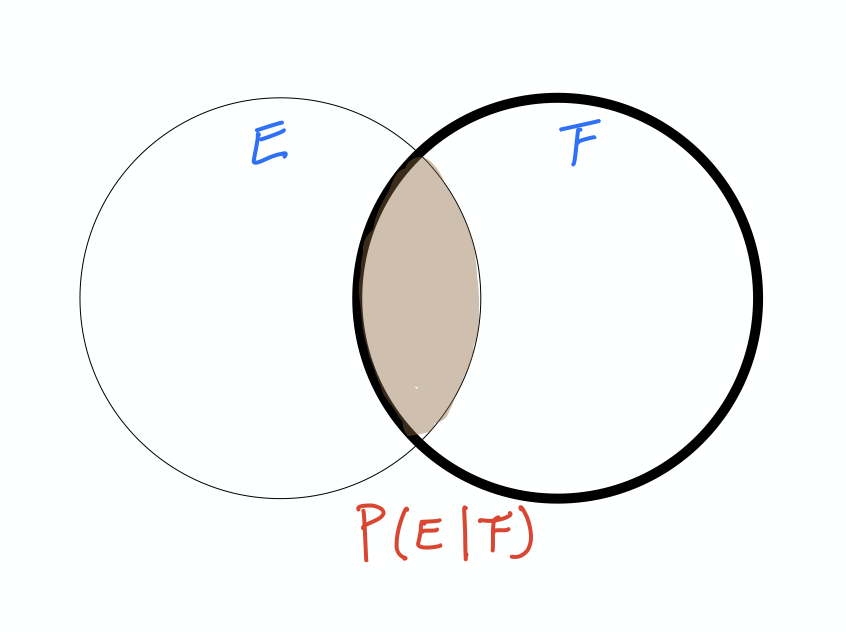
$$P(E, G) = 0 \neq \frac 1 2 \cdot \frac 1 4 = P(E) \cdot P(G)$$두 사건 $E$와 $F$의 독립/종속 여부를 모르고, $P(F) \neq 0$이라고 가정하자. 이때, 사건 $F$가 발생했다는 조건 하에서 사건 $E$가 발생할 확률을 조건부 확률이라 부르며 조건부 확률 $P(E|F)$는 아래와 같다.
$$P(E|F) = \frac{P(E,F)}{P(F)}$$위 식을 조금 변경하면 다음과 같다.
$$P(E,F) = P(E|F) \cdot P(F)$$따라서, $E$와 $F$가 서로 독립이라면 아래 결과를 얻으며,
$$P(E|F) = P(E)$$이것은 사건 $F$의 발생여부가 사건 $E$의 발생여부에 영향을 주지 않는다는 사실을 다시 확인해준다.
 |
 |
문제 1: 첫째가 딸이라는 조건 하에서 두 아이 모두 딸일 확률을 구해보자.
다음 두 사건을 대상으로 해서 조건부 확률을 계산하면 된다.
직관적으로 납득할만하다. 첫째가 딸이면, 두 아이 모두 딸일 확률은, 둘째가 딸일 확률과 같기 때문이다.
문제 2: 딸이 1명 이상일 때, 두 아이 모두 딸일 확률을 구해보자.
다음 두 사건을 대상으로 해서 조건부 확률을 계산하면 된다.
딸이 한 명 이상이라면, 세 가지 경우가 가능하다.
(딸, 아들), (아들, 딸), (딸, 딸)
이 중에 딸 둘인 경우의 확률이기에 1/3이 나온다.
한 가족 내 두 아이들의 성별 맞추기를 파이썬으로 시뮬레이션 할 수 있다.
import enum, random
class Kid(enum.Enum):
BOY = 0
GIRL = 1
def random_kid() -> Kid:
return random.choice([Kid.BOY, Kid.GIRL])
both_girls = 0
older_girl = 0
either_girl = 0
random.seed(0)
for _ in range(10000):
younger = random_kid()
older = random_kid()
if older == Kid.GIRL:
older_girl += 1
if older == Kid.GIRL and younger == Kid.GIRL:
both_girls += 1
if older == Kid.GIRL or younger == Kid.GIRL:
either_girl += 1
print("P(both | older):", both_girls / older_girl)
print("P(both | either): ", both_girls / either_girl)
P(both | older): 0.5007089325501317 P(both | either): 0.3311897106109325
두 사건 $E, F$에 대해 조건부 확률 $P(F|E)$가 알려져 있다고 가정하자. 이때 베이즈 정리를 이용하면 $P(E|F)$를 계산할 수 있다.
베이즈 정리의 공식은 다음과 같다.
$$ P(E|F) = \frac{P(F|E)\cdot P(E)}{P(F|E)\cdot P(E) + P(F|\neg E)\cdot P(\neg E)} $$위 식에서 $\neg E$는 사건 $E$가 발생하지 않는 경우의 사건을 가리킨다.
베이즈 정리를 유도하는 방법은 여기서는 소개하지 않는다. 대신에 아래 성질을 기억해 두어야 한다.
10,000명 중에 한 명이 걸리는 질병이 있다고 가정하자. 또한 다음 사실이 알려져 있다고 가정한다.
이 전제조건은 해당 질병에 걸리지 않은 사람을 판단할 때 양성으로 판단할 확률이 1%라는 사실을 의미한다.
이제 어떤 사람을 진단해 보니 해당 질병에 걸렸다는 진단이 나왔을 때, 그 사람이 진짜 그 질병에 걸렸을 확률을 구해보자.
다음 두 사건을 대상으로 해서 조건부 확률 $P(D|T)$를 계산하면 된다.
하지만 우리에게 알려진 확률은 다음과 같다.
따라서
$$ P(D|T) = \frac{P(T|D)\cdot P(D)}{P(T|D)\cdot P(D) + P(T|\neg D)\cdot P(\neg D)} $$의 실제 계산결과는 아래와 같다.
PT_D = 0.99
PD = 0.0001
PT_negD = 0.01
numerator = PT_D * PD
denominator = numerator + PT_negD * (1 - PD)
PD_T = numerator/denominator
print(PD_T)
0.00980392156862745
즉, 어떤 사람이 임의로 진단을 받아서 양성 판정이 나왔다 하더라도 그 사람이 정말로 질병을 갖고 있을 확률은 0.98%이며, 1%도 되지 않는다.
위 결과는 좀 놀랍다. 하지만 진단 받은 사람을 임의로 골랐기 때문에 위 결과가 성립한다. 만약에 진단받은 사람이 해당 질병의 징후를 보였다면 다른 조건부 확률을 계산해야 할 것이다.
하지만 아무런 징후도 없다고 가정한다면 위 결과를 다음과 같이 설명할 수 있다.
확률에 의해 100만명 중에 100명은 질병에 걸렸을 것이고 그중에 99명은 양성 판정을 받을 것이다. 반면에 나머지 99만 9천명은 질병에 걸리지 않았을 것이며, 그중 1%인 9,999 명만 양성 판정을 받을 것이다. 즉, 100만 명 중에 양성판정을 받을 사람 수는 (99 + 9999 = 10098) 명이다.
따라서 양성판정을 받은 10098 명 중에 진짜 질병을 갖고 있는 사람의 확률은 99/10098 = 0.0098이다.
99/(99 + 9999)
0.00980392156862745
확률분포는 사건들의 확률이 어떻게 분포되어 있는가를 말하며, 확률분포표 또는 확률밀도함수의 그래프를 이용하여 표현한다. 확률변수는 특정 확률분포와 연관되어 있는 사건들을 가리키는 변수이다.
확률분포는 이산 확률분포와 연속 확률분포로 나뉜다.
이산 확률분포는 동전 던지기와 같이 각각의 사건에 대해 확률을 계산해 주는 분포이다. 특정 사건 $x$의 확률을 $P(X=x)$ 표기한다. 여기서 $X$는 확률변수들을 대표하는 변수이다.
확률변수와 확률을 곱한 값을 모두 더하여 얻어지는 값을 기댓값이라 부른다.
$$E(X) = \sum x \cdot P(X=x)$$동전던지기에서 확률변수가 가리키는 사건은 동전의 앞면이 나오면 1, 뒷면이 나오면 0을 가리키게 할 수 있다. 그리고 각 확률변수의 확률은 정상적인 동전일 경우에 0.5이다.
| 사건(x) | 0 | 1 |
| P(X=x) | 0.5 | 0.5 |
그러면 기댓값 $E(X) = 0 \cdot 1/2 + 1 \cdot 1/2 = 0.5$이다.
동전던지기에서 확률변수가 가리키는 사건은 동전의 앞면이 나오면 100원을 얻고, 뒷면이 나오면 100원을 잃는 것을 가리키게 할 수 있다. 그리고 각 확률변수의 확률은 정상적인 동전일 경우에 0.5이다.
| 사건(y) | -100 | 100 |
| P(Y=y) | 0.5 | 0.5 |
그러면 기댓값 $E(Y) = -100 \cdot 1/2 + 100 \cdot 1/2 = 0$이다. 즉, 동전을 한 번 던질 때마다 75원을 받을 것으로 기대한다.
동전을 10번 던 져서 앞면이 나온 횟수를 확률변수가 가리킨다. 이런 확률변수의 확률분포는 이항분포라고 부른다.
| 사건(r) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| P(X=r) | P(X=0) | P(X=1) | P(X=2) | P(X=3) | P(X=4) | P(X=5) | P(X=6) | P(X=7) | P(X=8) | P(X=9) | P(X=10) |
단, 아래가 성립한다.
$$ \sum_{r=0}^{10} P(X=r) = 1, \qquad P(X=r) = \frac{10!}{r! \cdot (10-r)!} \cdot 2^{-10} $$실제로 계산해보면 기대값은 5이다. 즉, 동전을 10번 던지면 앞면이 5번 정도 나올 것으로 기대하며, 이는 우리가 기대하는 값과 동일하다.
from math import factorial
def P(r):
return (factorial(10) * 2**(-10)) / (factorial(r) * factorial(10-r))
EX = sum([r * P(r) for r in range(11)])
print(EX)
5.0
그리고 확률의 합은 항상 1이어야 한다.
sum(P(r) for r in range(11))
1.0
확률분포를 조건부 확률과 연계하여 정할 수 있다.
| 사건(x) | 0 | 1 | 2 |
| P(X=x) | 1/4 | 1/2 | 1/4 |
둘째 확률변수 $Y$는 딸이 최소 한 명일 때 전체 딸의 수를 가리킨다. 그러면 확률분포표는 다음과 같다.
| 사건(y) | 1 | 2 |
| P(Y=y) | 2/3 | 1/3 |
셋째 확률변수 $Z$는 첫째가 딸일 때 전체 딸의 수를 가리킨다. 그러면 확률분포표는 다음과 같다.
| 사건(z) | 1 | 2 |
| P(Z=z) | 1/2 | 1/2 |
동전 던지기와는 달리 키, 몸무게, 거리, 시간 등은 특정 값 각각에 대한 확률을 얘기하는 것은 의미가 없다. 왜냐하면 0이기 때문이다.
예를 들어, 버스가 정확히 1분 43초 만에 도착할 확률은 0이다. 또한 사람 한 명을 임의로 골라 키를 재었을 때 키가 정확히 1미터 71.2cm 일 확률 역시 0이다. 그리고 0과 1 사이의 임의의 실수 하나를 선택했을 때 그 숫자가 0.5232일 확률 역시 0이다.
반면에 버스가 앞으로 1분에서 2분 사이에 도착할 확률은 0이 아니며, 버스 운행시간에 따라 확률을 계산할 수 있다. 사람의 키와 0과 1 사이의 숫자를 맞추는 일도 구간을 지정하면 확률을 구할 수 있다.
이렇게 연속적인 값들에 대한 확률분포를 연속 확률분포로 부른다. 연속 확률분포에서는 특정 변수의 확률은 항상 0이다. 따라서 변수의 구간에 대한 확률을 계산한다.
0과 1 사이의 값을 동등한 비중으로 선택하도록 한 분포가 균등분포(uniform distribution)이다. 즉, 임의로 선택한 숫자가 구간 $a$와 $b$ 사이에 위치할 확률을 $b - a$이다. 단, $0 \le a < b \le 1$이다.
random.random() 함수가 0과 1 사이의 실수를 균등하게 무작위로 생성한다.
연속확률분포의 특정 구간에서의 확률은 보통 확률밀도함수(probability density function, pdf)의 적분값으로 계산된다.
주의: 우리가 직접 적분을 사용하지는 않는다.
예를 들어, 균등분포의 확률밀도함수는 단순하다.
def uniform_pdf(x: float) -> float:
return 1 if 0 <= x < 1 else 0
import matplotlib.pyplot as plt
xs = [x / 10.0 for x in range(-10, 20)]
plt.plot(xs,[uniform_pdf(x) for x in xs],'-',label='mu=0,sigma=1')
plt.show()
확률변수의 값이 특정 값보다 작을 확률을 계산해주는 함수를 누적분포함수(cummulative distribution function, cdf)라 부른다.
균등분포의 누적분포함수는 다음과 같다.
def uniform_cdf(x: float) -> float:
if x < 0: return 0
elif x < 1: return x
else: return 1
plt.plot(xs,[uniform_cdf(x) for x in xs],'-',label='mu=0,sigma=1')
plt.show()
정규분포는 연속 확률분포를 대표한다. 정규분포의 확률밀도함수는 종 모양의 그래프를 가진다. 정규분포는 평균값 뮤($\mu$)와 표준편차 시그마($\sigma$)에 의해 결정된다.
평균값이 $\mu$, 표준편차가 $\sigma$인 정규분포 $X$를 보통 아래와 같이 표기한다.
$$X \sim N(\mu, \sigma^2)$$아래 그림에서 정규분포의 확률밀도함수가 $\mu$와 $\sigma$에 의존하는 것을 볼 수 있다.
import math
SQRT_TWO_PI = math.sqrt(2 * math.pi)
def normal_pdf(x: float, mu: float = 0, sigma: float = 1) -> float:
return (math.exp(-(x-mu) ** 2 / 2 / sigma ** 2) / (SQRT_TWO_PI * sigma))
import matplotlib.pyplot as plt
xs = [x / 10.0 for x in range(-50, 50)]
plt.plot(xs,[normal_pdf(x,sigma=1) for x in xs],'-',label='mu=0,sigma=1')
plt.plot(xs,[normal_pdf(x,sigma=2) for x in xs],'--',label='mu=0,sigma=2')
plt.plot(xs,[normal_pdf(x,sigma=0.5) for x in xs],':',label='mu=0,sigma=0.5')
plt.plot(xs,[normal_pdf(x,mu=-1) for x in xs],'-.',label='mu=-1,sigma=1')
plt.legend()
plt.title("Various Normal pdfs")
plt.show()
정규분포의 누적분포함수는 직접 계산하기 어렵다. 다만 그래프는 아래와 같으며, 역시 $\mu$와 $\sigma$에 의존한다.
def normal_cdf(x: float, mu: float = 0, sigma: float = 1) -> float:
return (1 + math.erf((x - mu) / math.sqrt(2) / sigma)) / 2
xs = [x / 10.0 for x in range(-50, 50)]
plt.plot(xs,[normal_cdf(x,sigma=1) for x in xs],'-',label='mu=0,sigma=1')
plt.plot(xs,[normal_cdf(x,sigma=2) for x in xs],'--',label='mu=0,sigma=2')
plt.plot(xs,[normal_cdf(x,sigma=0.5) for x in xs],':',label='mu=0,sigma=0.5')
plt.plot(xs,[normal_cdf(x,mu=-1) for x in xs],'-.',label='mu=-1,sigma=1')
plt.legend(loc=4) # bottom right
plt.title("Various Normal cdfs")
plt.show()
표준정규분포는 $\mu = 0$이고 $\sigma = 1$인 정규분포를 가리킨다. 위 그림에서 녹색 점선으로 표시된 그래프가 표준정규분포의 확률밀도함수 그래프이다.
정규분포 $X$가 주어졌다고 가정하자.
$$X \sim N(\mu, \sigma^2)$$그러면 표준화 과정을 통해 표준정규분포로 만들어 확률 계산을 보다 쉽게 할 수 있다.
$$Z = \frac{X -\mu}{\sigma}$$그러면 다음이 성립한다.
$$Z \sim N(0, 1)$$표준정규분포를 이용한 확률계산이 매우 쉽다. 앞서 제시된 누적분포함수를 이용할 수도 있지만 일상에서는 표준정규분포 확률테이블을 이용하면 쉽게 확률을 구할 수 있다.
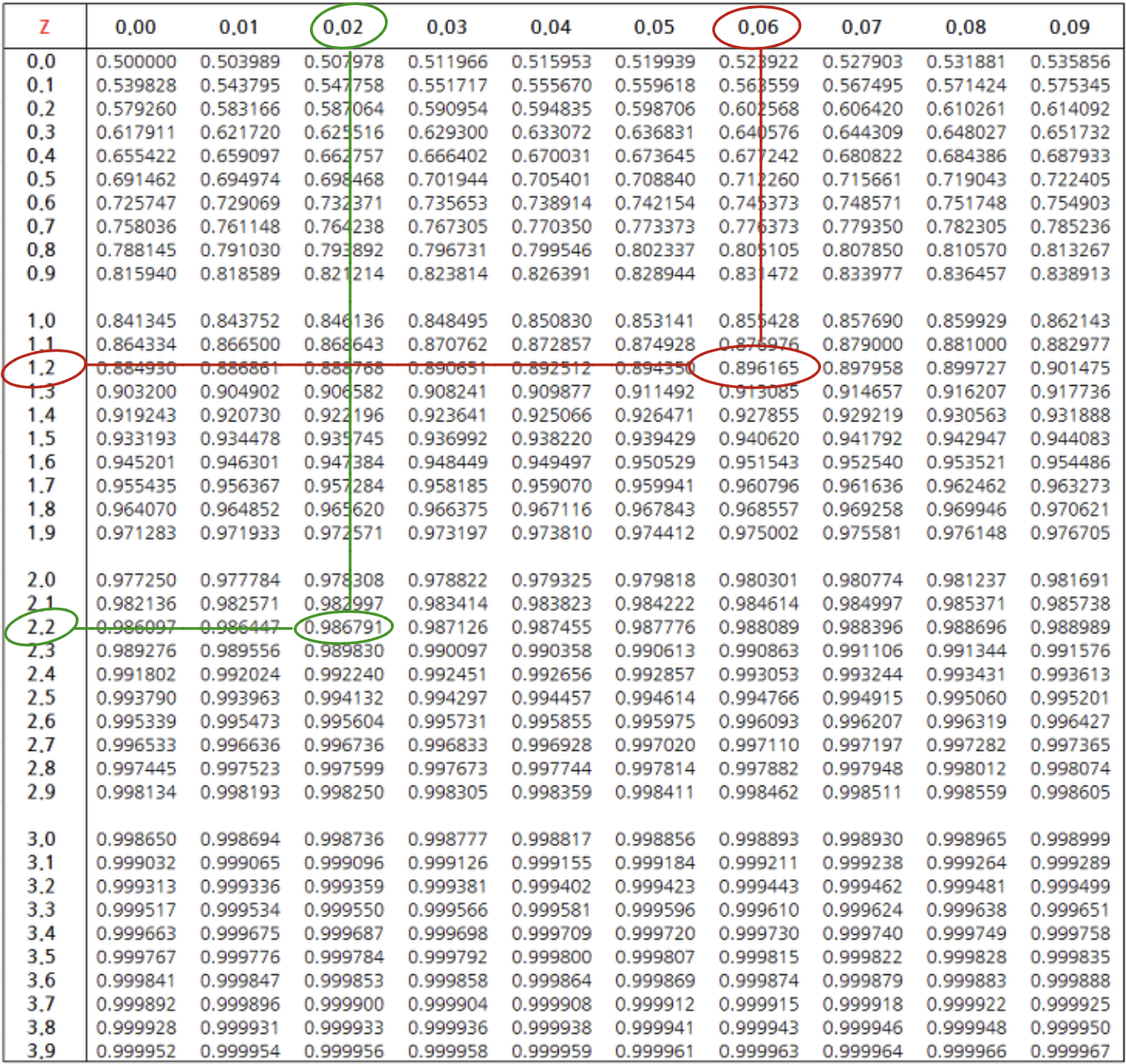
$X \sim N(0, 1)$라 하자. 이제 다음 확률을 구해보자
P126 = normal_cdf(1.26)
P222 = normal_cdf(2.22)
print(f"P126: {P126}",
f"P222: {P222}", sep='\n')
P126: 0.8961653188786995 P222: 0.9867906161927438
종종 특정 확률을 갖는 구간을 찾고자 할 때가 있다. 그럴 때는 누적분포함수의 역함수를 이용하면 된다. 하지만 역함수를 직접 구현하기는 어렵다. 아래 함수는 이진 검색 기술을 응용하여 구현하였다. 이진 검색을 잘 이해한다면 함수 본체를 이해할 수 있을 것이다.
def inverse_normal_cdf(p: float,
mu: float = 0,
sigma: float = 1,
tolerance: float = 0.00001) -> float:
if mu != 0 or sigma != 1:
return mu + sigma * inverse_normal_cdf(p, tolerance=tolerance)
low_z = -10.0
hi_z = 10.0
while hi_z - low_z > tolerance:
mid_z = (low_z + hi_z) / 2
mid_p = normal_cdf(mid_z)
if mid_p < p:
low_z = mid_z
else:
hi_z = mid_z
return mid_z
예를 들어, $P(X < r) = 0.896165$이 되는 $r$을 알괴 싶다면 위 함수를 적용하면 된다.
inverse_normal_cdf(0.896165)
1.2600040435791016
앞서 구한 $P(X < 1.26)$과 거의 비슷한 값을 반환함을 확인하였다.
중심극한정리란 어떤 확률분포가 비록 정규분포가 아니라 하더라도 해당 확률분포를 반복적으로 적당히 많이 실행한 결과의 평균에 대한 확률분포는 정규분포를 따른다는 정리이다.
예를 들어, 동전 던지기 확률분포를 살펴보자. 정상적인 동전을 10번 던지면 앞서 계산해 보았듯이 5번 정도 앞면이 나올 것으로 기대한다. 하지만 실제로 동전을 10번 던져서 앞면이 매번 5번 나오지는 않는다. 심지어 확률이 낮기는 하지만 앞면이 한 번도 나오지 않거나, 열 번 모두 앞면이 나오는 경우도 볼 수 있을 것이다. 그리고 앞면이 2, 3 번 나오는 경우는 어렵지 않게 접할 것이다.
그런데 동전을 100번쯤 던지면 앞면이 나오는 횟수가 50번 정도 나올 것이다. 그리고 앞면이 20번 이하로 나올 확률은 거의 없으며, 그것을 기대하는 사람도 거의 없을 것이다.
또한 동전을 100번 던져서 앞면이 나오는 회수의 확률분포는 정규분포를 따른다. 왜 그럴까? 이유는 모르지만 그렇게 되는 것을 중심극한정리라 부른다.
동전 던지기는 이항분포의 한 예제이다.
이항분포는 어떤 일을 한 번 시행했을 때 특정 사건이 발생할 것인가를 반복적으로 확인하는 베르누이 분포를 반복적으로 시행하여 얻어진 확률분포이다.
동전던지기의 경우는 앞면이 나오거나 그렇지 않거나를 반복적으로 확인하는 이항분포이며, 특정 사건이 발생할 확률이 $p$이고, 반복횟수가 $n$인 이항분포는 아래와 같이 표기한다.
$$X \sim B(n, p)$$예를 들어, 정상적인 동전을 10번 던지는 이항분포는 다음과 같이 표기한다.
$$X \sim B(10, \frac 1 2)$$이제 이항분포 $X \sim B(n,p)$가 다음 조건을 만족시킨다고 가정하자.
$$n\cdot p > 5 \quad \text{and} \quad n\cdot (1-p) > 5$$그러면 다음이 성립한다.
$$X \sim N(n\cdot p, n\cdot p\cdot (1-p))$$즉, 평균이 $n\cdot p$ 이고 표준편차가 $\sqrt{n\cdot p\cdot (1-p)}$ 인 정규분포를 따른다.
예를 들어, 동전을 100번 던졌을 때 50번 정도 앞면이 나오는 것을 모의실험해서 확인할 수 있다.
import random
def bernoulli_trial(p: float) -> int:
"""Returns 1 with probability p and 0 with probability 1-p"""
return 1 if random.random() < p else 0
def binomial(n: int, p: float) -> int:
"""Returns the sum of n bernoulli(p) trials"""
return sum(bernoulli_trial(p) for _ in range(n))
from collections import Counter
def binomial_histogram(p: float, n: int, num_points: int) -> None:
"""Picks points from a Binomial(n, p) and plots their histogram"""
data = [binomial(n, p) for _ in range(num_points)]
# use a bar chart to show the actual binomial samples
histogram = Counter(data)
plt.bar([x - 0.4 for x in histogram.keys()],
[v / num_points for v in histogram.values()],
0.8,
color='0.75')
mu = p * n
sigma = math.sqrt(n * p * (1 - p))
# use a line chart to show the normal approximation
xs = range(min(data), max(data) + 1)
ys = [normal_cdf(i + 0.5, mu, sigma) - normal_cdf(i - 0.5, mu, sigma)
for i in xs]
plt.plot(xs,ys)
plt.title("Binomial Distribution vs. Normal Approximation")
plt.show()
binomial_histogram(0.5,100,10000)
위 그래프는 동전 100번 던지기를 10,000번 반복했을 때, 앞면이 나오는 횟수에 대한 확률분포를 보여준다. 모의실험 결과 역시 거의 정확하게 아래 정규분포를 보여준다. ($100 \cdot 0.5 = 50 > 5$)
$$X \sim n(50, 5^2)$$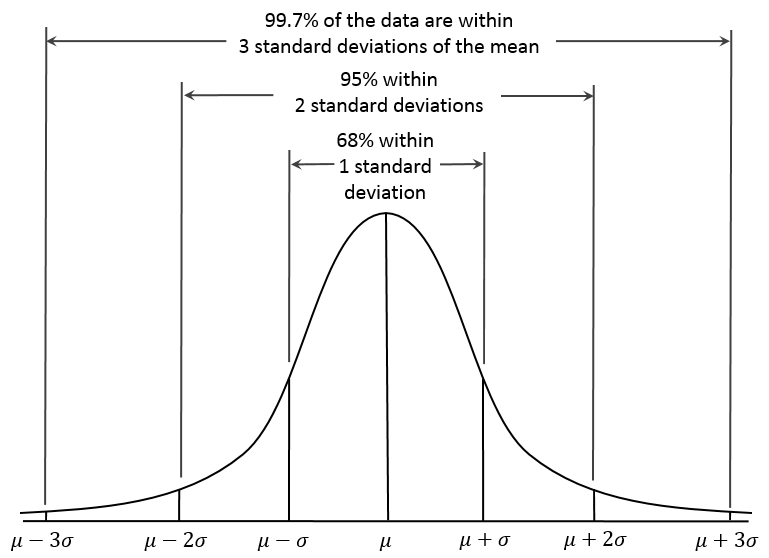
출처:위키북스
동전을 100번 던져 앞면이 20번 미만 나올 확률은 사실상 0%이다. 확인은 다음과 같이 할 수 있다.
동전 던지기가 정규분포 $X = N(50, 5^2)$를 따른다. 따라서 표준화를 이용하여 $P(X < 20)$ 계산할 수 있다.
$$P(X < 20) = P(Z < \frac{20-50}{5}) = P(Z < -6) < 10^{-10}$$아래 계산에서 확인되며, 위 표준정규분포 확률테이블을 이용해서는 확인할 수 있다. 확률테이블에서 확인되지 않는 값은 사실상 0이라고 생각하면 된다.
normal_cdf(-6)
9.865876449133282e-10