기본 자료형: 집합과 사전¶

집합¶

set 자료형은 집합에 해당하는 자료형이며, 수학에서 배운 집합 개념과 동일하다.

원소들 사이의 순서가 없다.
중복된 원소를 인정하지 않는다.

primes_below_10 = {2, 3, 7, 5, 7, 3}
primes_below_10

{2, 3, 5, 7}

원소의 개수는 len 함수를 이용하여 확인한다.

len(primes_below_10)

4

공집합은 set()으로 생성하며, 원소 추가는 add 메소드를 활용한다.

s = set()
s.add(1)
s.add(2)
s.add(2)

print(s)

{1, 2}

원소의 포함여부는 in 연산자를 활용하여 확인한다.

2 in s

True

3 in s

False

집합 자료형 사용 이유¶

예제¶

리스트에 중복으로 포함된 항목을 쉽게 제거할 수 있다.

item_list = [1, 2, 3, 1, 2, 3]

item_set = set(item_list) 
distinct_item_list = list(item_set)

print(distinct_item_list)

[1, 2, 3]

예제¶

리스트에 중복으로 포함된 항목이 존재하는가를 쉽게 판단할 수 있다. 예를 들어, 아래 함수는 중복 함수의 포함여부를 판단해준다.

def has_duplicates(t):
    return len(set(t)) < len(t)

has_duplicates(item_list)

True

예제¶

길이가 매우 긴 리스트를 대상으로 항목의 존재여부를 판단할 때 집합 자료형으로 형변환을 하면 매우 빠르게 해결할 수 있다.

hundreds_of_other_words = []  # 매우 긴 리스트라 상상한다.
stopwords_list = ["a", "an", "at"] \
                + hundreds_of_other_words + ["yet", "you"]

print("zip" in stopwords_list)     # 확인 과정이 느리다.

stopwords_set = set(stopwords_list)
print("zip" in stopwords_set)      # 매우 빠르게 확인한다.

False
False

예제¶

부분집합 관계를 이용할 수 있다. 예를 들어, 아래 함수는 첫째 인자의 리스트에 포함된 모든 원소가, 둘째 인자의 리스트에 항목으로 포하되는지 여부를 판단한다.

주의: <= 연산자는 집합을 대상으로 할 경우 부분집합 관계를 결정한다.

def sublist(list1, list2):
    return set(list1) <= set(list2)

sublist(item_list, distinct_item_list)

True

사전¶

안내: Think Python 11장 내용의 일부를 번역 및 요약수정하여 정리한 내용입니다.

사전 자료값은 일종의 쌍들의 집합이며, 각 쌍은 키(key)와 값(value)으로 이루어져 있다.

키(key): 영어사전의 각 영어단어에 해당함.
값(value): 특정 영어단어의 뜻에 해당함.

예를 들어, 전자영어사전에서 'school'이란 단어의 뜻을 물으면 '학교'라는 뜻을 알려주는데 여기서 'school'이 키에 해당하고 '학교'가 값에 해당한다. 따라서 전자영어사전은 이러한 키와 값들의 쌍을 무수히 많이 모아놓은 집합이라고 생각할 수 있다.

항목¶

사전에 포함된 항목은 키와 값으로 이루어진 쌍이다. 각각의 항목은 키와 그 키와 연관된 값들에 대한 정보라고 이해하면 된다.

여기서는 영한사전을 생성하는 예제를 통해 사전 자료형의 활용을 설명하고자 한다.

빈 사전 생성¶

먼저 빈 사전을 생성한다.

빈 사전을 생성하려면 dict 함수를 활용하거나 단순히 아래와 같이 선언하면 된다.

eng2kr = dict()
print(eng2kr)

{}

또는

eng2kr = {}
print(eng2kr)

{}

주의: 중괄호({})는 빈 딕셔너리를 나타낸다.

항목 추가¶

사전에 항목을 추가하려면 키와 값의 관계를 대괄호 연산자를 이용하여 지정하면 된다. 예를 들어, 영단어 one과 한글 뜻 일, 하나를 연관지으려면 다음과 같이 한다.

eng2kr['one'] = '일, 하나'

사전에 포함된 내용을 확인하면 키와 값 사이에 콜론이 들어간 키와 값의 쌍을 볼 수 있다.

print(eng2kr)

{'one': '일, 하나'}

항목을 하나 더 추가해보자.

eng2kr['three'] = '삼, 셋'

print(eng2kr)

{'one': '일, 하나', 'three': '삼, 셋'}

사전 선언¶

아래와 같이 사전을 바로 선언할 수도 있다.

dict_exp = {'one':'일, 하나', 'two':'이, 둘', 'three':'삼, 셋'}

print(dict_exp)

{'one': '일, 하나', 'two': '이, 둘', 'three': '삼, 셋'}

항목의 순서¶

'eng2kr'에 항목을 하나 더 추가해보자.

eng2kr['two'] = '이, 둘'

print(eng2kr)

{'one': '일, 하나', 'three': '삼, 셋', 'two': '이, 둘'}

영어사전에 어떤 단어가 몇 번째에 위치하는가는 전혀 중요하지 않다. 대신에 어떤 키가 사용되었는가만 중요하다.

대괄호(`[]`) 연산자¶

대괄호 연산자는 항목을 추가할 때와 함게 항목을 확인하거나 업데이트 할 때도 사용한다. 예를 들어, 'one'에 대응하는 값을 확인하고자 하면 다음과 같이 대괄호를 사용하는 인덱싱을 이용한다.

print(eng2kr['one'])

일, 하나

키와 연관된 값을 업데이트 하려면 새롭게 지정하면 된다.

eng2kr['one'] = '일, 하나, 한번, 유일한'
print(eng2kr)

{'one': '일, 하나, 한번, 유일한', 'three': '삼, 셋', 'two': '이, 둘'}

만약 키가 사전에 사용되지 않았으면 오류(KeyError)가 발생한다.

print(eng2kr['four'])

---------------------------------------------------------------------------
KeyError                                  Traceback (most recent call last)
<ipython-input-24-bb50ad42a120> in <module>
----> 1 print(eng2kr['four'])

KeyError: 'four'

'len' 함수¶

사전에 포함된 항목의 개수를 확인시켜주는 함수이다.

len(eng2kr)

3

'in' 연산자¶

특정 키가 사전에 사용되었는지 여부를 확인한다.

'one' in eng2kr

True

'four' in eng2kr

False

사전 자료형 메서드¶

`keys` 메서드¶

사전에 사용된 키들을 모두 모아서 리스트와 비슷한 자료형을 만들어서 리턴한다.

주의: 리스트와는 다르지만 매우 비슷하다.

keys = eng2kr.keys()

print(keys)

dict_keys(['one', 'three', 'two'])

아래 두 코드는 동일한 일을 수행한다.

'one' in eng2kr

True

'one' in eng2kr.keys()

True

`values` 메서드¶

사전에 사용된 값들을 모두 모아서 리스트와 비슷한 자료형을 만들어서 리턴한다.

주의: 리스트와는 다르지만 매우 비슷하다.

values = eng2kr.values()
print(values)

dict_values(['일, 하나, 한번, 유일한', '삼, 셋', '이, 둘'])

값으로 사용되었는가 여부를 이용하려면 values 메서드를 활용하면 된다.

'이' in eng2kr.values()

False

'사' in eng2kr.values()

False

`items` 메서드¶

사전에 포함된 항목들을 순서쌍들의 리스트로 변환한다. 각각의 순서쌍은 키와 값으로 이루어진, 즉 길이가 2인 튜플이다.

주의: 리스트와는 다르지만 매우 비슷하다.

values = eng2kr.items()
print(values)

dict_items([('one', '일, 하나, 한번, 유일한'), ('three', '삼, 셋'), ('two', '이, 둘')])

사전의 항목을 튜플로 하나씩 확인해보자. 항목들이 길이가 2인 튜플로 구성되기에 변수 두 개에 각각 할당할 수 있다.

for eng, kor in eng2kr.items():
    print(f"{eng}의 뜻은 {kor}입니다.")

one의 뜻은 일, 하나, 한번, 유일한입니다.
three의 뜻은 삼, 셋입니다.
two의 뜻은 이, 둘입니다.

영어 단어에 여러 뜻이 있을 수 있기 때문에 그것을 보다 상세히 보여줄 수도 있다. 그러기 위해 문자열을 split과 join 메서드를 활용한다.

참고: split/join 메서드의 활용은 문자열 나누기/합치기에 좀 더 다양한 예제가 있음.

for eng, kor in eng2kr.items():
    meaning = kor.split(', ')
    print(f"{eng}의 뜻은 {' 또는 '. join(meaning)}입니다.")

one의 뜻은 일 또는 하나 또는 한번 또는 유일한입니다.
three의 뜻은 삼 또는 셋입니다.
two의 뜻은 이 또는 둘입니다.

예제: 다이빙 기록과 사전 자료형¶

연관배열 활용에서 다룬 다이빙 기록을 사전 자료형으로 저장하는 함수는 다음과 같다.

def scoreDict(fileName):
    try:
        result_f = open(fileName, 'r') 
    except FileNotFoundError:
        print("열고자 하는 파일이 존재하지 않습니다.")

    score_dict = dict() 

    for line in result_f: 
        name, score = line.split() 
        try:
            score_dict[float(score)] = name
        except:
            continue
    result_f.close() 

    return score_dict

위 함수를 5m 다이빙 기록과 함께 호출하면 기록을 사전 자료형으로 저장할 수 있다.

scores = scoreDict('./data/results5m.txt')
print(scores)

{7.13: '권준기', 8.55: '김세윤', 9.02: '나진서', 8.35: '마동탁', 7.86: '서길석', 8.17: '이준용', 9.33: '이차승', 7.11: '차승연', 8.57: '표방호', 8.93: '한석준'}

그런데 scoreDict 함수는 선수들의 성적을 키로, 해당 성적을 낸 선수 이름을 값으로 사용한다. 그렇게 한 이유는 정렬을 이용하여 등수를 정하기 위해서 였다.

여기서는 선수이름을 키로, 해당 선수의 성적을 값으로 활용해보자. 그러기 위해 scoreDict를 아래와 같이 약간 수정하면 된다.

def nameScoreDict(fileName):
    try:
        result_f = open(fileName, 'r') 
    except FileNotFoundError:
        print("열고자 하는 파일이 존재하지 않습니다.")

    nameScore_dict = dict()                   # 이름을 키로 사용 암시

    for line in result_f: 
        name, score = line.split() 
        try:
            nameScore_dict[name] = float(score)   # 이름을 키로, 성적을 값으로.
        except:
            continue
    result_f.close() 

    return nameScore_dict

5m 다이빙 기록을 다시 읽어온다.

nameScores = nameScoreDict('./data/results5m.txt')
print(nameScores)

{'권준기': 7.13, '김세윤': 8.55, '나진서': 9.02, '마동탁': 8.35, '서길석': 7.86, '이준용': 8.17, '이차승': 9.33, '차승연': 7.11, '표방호': 8.57, '한석준': 8.93}

이제 선수 이름을 지정하면 해당 선수의 점수를 인덱싱을 활용하여 확인할 수 있다.

nameScores['권준기']

7.13

nameScores['이준용']

8.17

반복문과 사전¶

사전을 for 반복문에 사용하면 사전의 키를 기준으로 반복문을 실행한다.

아래 예제는 nameScores에 저정된 값들을 파일의 내용과 동일한 모양으로 하나씩 출력한다.

for key in nameScores:
    print(key, nameScores[key])

권준기 7.13
김세윤 8.55
나진서 9.02
마동탁 8.35
서길석 7.86
이준용 8.17
이차승 9.33
차승연 7.11
표방호 8.57
한석준 8.93

아래 코드는 위 코드와 동일한 기능을 수행한다.

for key in nameScores.keys():
    print(key, nameScores[key])

권준기 7.13
김세윤 8.55
나진서 9.02
마동탁 8.35
서길석 7.86
이준용 8.17
이차승 9.33
차승연 7.11
표방호 8.57
한석준 8.93

예제: 카운터¶

문자열에 사용된 각각의 문자가 몇 번씩 사용되었는지를 확인하는 함수를 사전을 이용하여 쉽게 구현할 수 있다.

def histogram(word):
    counts = dict()
    for c in word: 
        if c not in counts:   # 알파벳이 처음 사용된 경우
            counts[c] = 1     # counts 사전에 키와 카운트 값 추가
        else:                 # 알파벳이 이미 사용된 경우
            counts[c] += 1    # 기존의 카운트 값 1 증가
    return counts

histogram('HelloPython')

{'H': 1, 'e': 1, 'l': 2, 'o': 2, 'P': 1, 'y': 1, 't': 1, 'h': 1, 'n': 1}

아래에 정의된 함수 print_hist는 각 키와 대응하는 값을 인쇄한다.

def print_hist(a_dict):
    for key in a_dict:
        print(key, a_dict[key])

앞서 구현한 'histogram' 함수의 리턴값을 활용하면 다음과 같다.

countHelloPython = histogram('HelloPython')
print_hist(countHelloPython)

H 1
e 1
l 2
o 2
P 1
y 1
t 1
h 1
n 1

동적계획, 리스트, 사전¶

피보나찌 수열¶

피보나찌(Fibonacci) 수열은 아래와 같이 전개된다.

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

즉, 수열의 첫째, 둘째 항목은 1이며, 셋째 항목은 첫째와 둘째 항목의 합, 넷째 항목은 둘째와 셋째 항목의 합, 등으로 진행된다. n이 2보다 클 경우, 이를 일반화하면 (n) 번째 항목은 (n-1) 번째 항목과 (n-2) 번째 항목의 합이며, 이를 수식으로 표현하면 다음과 같다.

fib(0)   = 1 
fib(1)   = 1 
fib(n) = fib(n-1) + fib(n-2)

재귀함수를 이용하면 쉽게 fib 함수를 구현할 수 있다.

def fib(n):
    if n in {0, 1}:
        return 1
    else:
        return fib(n-1) + fib(n-2)

실제로 잘 작동하는 것으로 보인다.

fib(0)

1

fib(1)

1

fib(2)

2

fib(3)

3

fib(5)

8

fib(10)

89

그런데 40번째 피보나찌 수 계산이 올래 걸릴 수 있다. 지금 사용하는 컴퓨터로 20초 이상 걸린다. 현재 사용된 컴퓨터 사양은 다음과 같다.

cpu: 3.6 GHz Quad-Core Intel Core i7
메모리: 16 GB 2400 MHz DDR4

주의:

실행시간을 측정하기 위해 time 모듈의 time 함수를 활용한다.
int 함수를 부동소수점을 인자로 사용하면 소수점 이하를 버린다.

import time                              # time 모듈 불러오기

start_time = time.time()                 # 실행 시작 시간 기억
fib(39)
end_time = time.time()                   # 실행 종료 시간 기억

elapsed_time = end_time - start_time
print(f'약 {int(elapsed_time)}초 걸렸습니다.')

약 26초 걸렸습니다.

하지만 1,000번째 피보나찌 수를 구하려는 시도는 웬만하면 하지 않는 게 좋다. 대부분 중간에 오류가 발생하거나 아니면 매우 오래 걸릴 수 있기 때문이다. 실제로 fib(n)을 계산하기 위해 fib 함수를 대략 $2^{n-1}$번 호출해야 한다. 예를 들어, fib(5)를 계산하기 위해 fib 함수를 15번 호출했다.

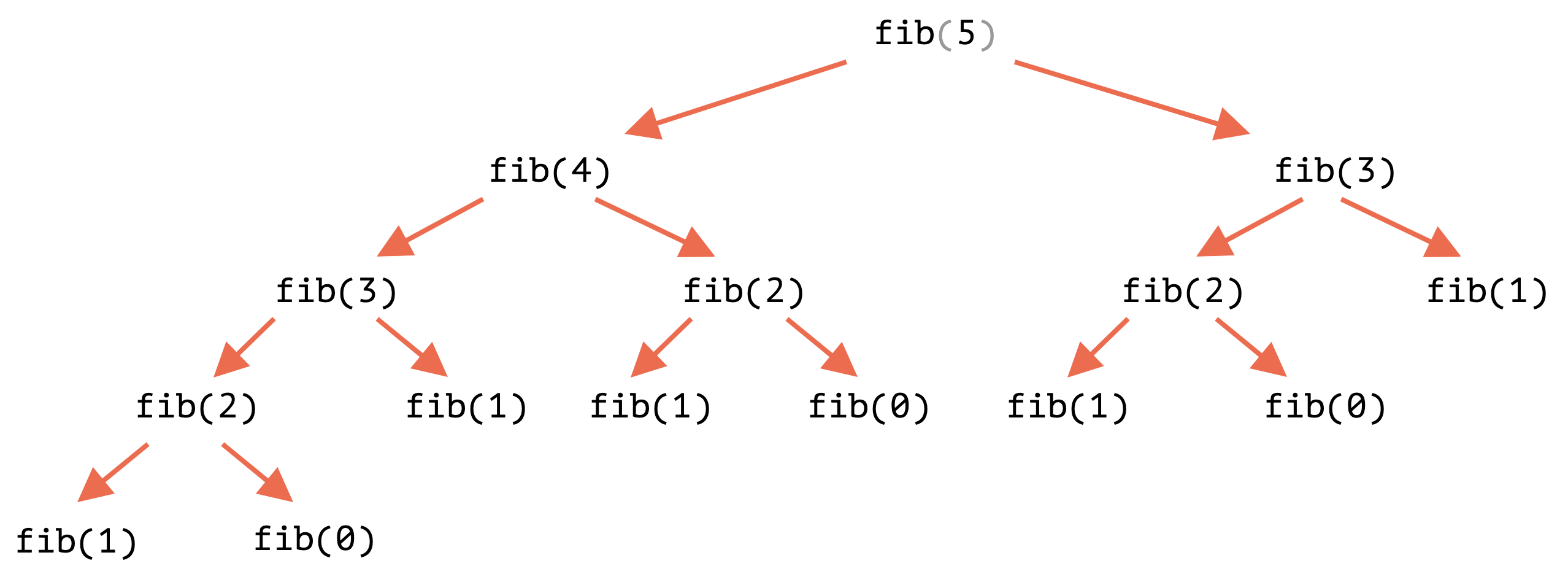
<그림 출처: 피보나찌 수 계산하기>

PythonTutor: 피보나찌 재귀함수에서 fib 함수의 인자를 변경해 보면서 실행을 시도해 보면 계산을 얼마나 많이 하고, 또 메모리를 얼마나 많이 사용하는지 눈으로 확인할 수 있다.

참고로 현재 Python Tutor에서 인자로 사용할 수 있는 한계는 10이다. 실제로

n = 9: 438번의 수행 단계 필요
n = 10: 710번의 수행 단계 필요

n > 10에 대해서는 PythonTutor 서버의 제한 때문에 실행되지 않는다.

동적계획과 리스트¶

재귀로 구현된 fib 함수의 근본적인 문제는 PythonTutor 예제에서 확인할 수 있듯이 반복적인 계산을 너무 많이 하는 것이다. 무엇보다도 n=39와 같은 작은 인자에 대해서 20초 이상 걸리는 계산은 문제가 많으며, 좀 더 큰 인자는 아예 계산을 할 수도 없다.

이에 대한 해결책을 동적계획(dynamic programming)이 제공한다. 동적계획은 반복적인 계산을 하지 않는다. 예를 들어,fib(5)를 계산하려면 fib(4), fib(3), fib(2) fib(1), fib(0) 등을 탑다운(top-down) 방식으로 계산해야 한다. 하지만 fib(0), fib(1), fib(2), fib(3), fib(4), fib(5) 등을 바텀업(bottom-up) 방식으로 계산하여 저장하는 방식을 사용하면 보다 빠르고 효율적으로 계산할 수 있다. 이런 방식을 동적계획이라 부른다.

이제 동적계획 방식으로 피보나찌 수열을 계산하는 함수를 구현해보자. 이미 계산된 피보나찌 수를 기억하기 위해 리스트를 활용한다.

먼저 아래와 같이 n 번째 피보나찌 수를 (n-1) 번 인덱스의 값으로 저장하는 방식을 사용할 수 있다.

def fibListLong(n):
    known_nums = [1, 1]                           # 첫번째, 두번재 피보나찌 수
    for k in range(2, n+1):                        
        res = known_nums[k-1] + known_nums[k-2]   # (k+1) 번째 피보나찌 수 계산
        known_nums.append(res)                    # k번 인덱스의 값이 (k+1) 번째 피보나찌 수
    return known_nums[-1]                         # 마지막 항목 출력

위와 같이 하면 40번째 피보나찌 수를 단번에 구해준다.

fibListLong(39)

102334155

심지어 1,001 번째 값도 금방 구한다.

fibListLong(1000)

70330367711422815821835254877183549770181269836358732742604905087154537118196933579742249494562611733487750449241765991088186363265450223647106012053374121273867339111198139373125598767690091902245245323403501

실험 결과 십만번 째 피보나찌 수도 금방 구한다.

start_time = time.time()                
fibNum100000 = fibListLong(100000)
end_time = time.time()                  

elapsed_time = end_time - start_time
print(f'약 {elapsed_time}초 걸렸습니다.')

약 0.33864307403564453초 걸렸습니다.

그런데 백만번째 피보나찌 수는 계산하지 못한다. 이유는 known_nums가 가리키는 리스트의 길이가 점점 길어지면서 동시에 항목에 사용되는 값들 역시 매우 큰 수가 되기 때문이다. 실제로 십만일번째 피보나찌 수는 다섯 화면에 걸쳐서 표기될 정도로 크다.

위 함수를 약간 업그레이드 할 수 있다. 피보나찌 수를 계산하기 위해 필요한 거는 이전에 계산된 두 개의 수 뿐이다. 따라서 그때까지의 모든 수를 기억할 필요가 없다. 이 아이디어를 이용하여 아래와 같이 구현하면 백만번째 피보나찌 수도 계산할 수 있다.

def fibList(n):
    known_nums = [1, 1]                         # 첫번째, 두번재 피보나찌 수
    for k in range(2, n+1):
        res = known_nums[1] + known_nums[0]     # 새로운 피보나찌 수 계산
        known_nums[0] = known_nums[1]           # 리스트 업데이트
        known_nums[1] = res
    return known_nums[1]                        # 둘째 항목 출력

fibList(1000)

70330367711422815821835254877183549770181269836358732742604905087154537118196933579742249494562611733487750449241765991088186363265450223647106012053374121273867339111198139373125598767690091902245245323403501

십만일번째 피보나찌 수도 눈깜빡할 사이에 계산한다. 바로 출력하면 너무 큰 수이기에 변수에 할당하는 식으로 해서 계산이 가능한지만 확인해보자.

start_time = time.time()
fibNum100000 = fibList(100000)
end_time = time.time()  

elapsed_time = end_time - start_time
print(f'약 {elapsed_time}초 걸렸습니다.')

약 0.19435954093933105초 걸렸습니다.

백만일번째 피보나찌 수도 10여초 만에 계산해준다.

start_time = time.time()
fibNum1M = fibList(1000000)
end_time = time.time()  

elapsed_time = end_time - start_time
print(f'약 {elapsed_time}초 걸렸습니다.')

약 10.604944944381714초 걸렸습니다.

천만일번째 수는 꽤 오래 걸린다. 몇 분 기다려도 계속 계산중이라 정지시켰다.

동적계획과 사전¶

앞서 길이가 2인 리스트를 사용하여 피보나찌 수를 업데이트 하면서 계산하였다. 동일한 아이디어를 사전을 이용하여 구현할 수 있다. 실행 시간과 능력은 기본적으로 fibList와 동일하다.

def fibDict(n):
    known_nums = {0:1, 1:1}
    for k in range(2, n+1):
        res = known_nums[1] + known_nums[0]
        known_nums[0] = known_nums[1]
        known_nums[1] = res
    return known_nums[1]

start_time = time.time()
fibNum100000 = fibDict(100000)
end_time = time.time()  

elapsed_time = end_time - start_time
print(f'약 {elapsed_time}초 걸렸습니다.')

약 0.13864493370056152초 걸렸습니다.

start_time = time.time()
fibNum1M = fibDict(1000000)
end_time = time.time()  

elapsed_time = end_time - start_time
print(f'약 {elapsed_time}초 걸렸습니다.')

약 10.598241329193115초 걸렸습니다.

처리속도: `in` 연산자¶

리스트에서 사용되는 in 연산자와 사전에서 사용되는 in 연산자는 내부적으로 서로 다르게 작동한다. 여기서는 처리속도 관련해서만 설명한다.

리스트의 in 연산자 검색 속도: 평균적으로 사용되는 리스트의 길이에 비례
사전의 in 연산자 검색 속도: 평균적으로 사전의 길이에 상관없음. 다만 최악의 경우 길이에 비례.

자세한 내용은 시간 복잡도를 참조할 수 있다.

연습문제¶

아래 기준을 만족하는 has_duplicates 함수를 구현하라.
- 하나의 리스트를 입력받는다.
- 리스트에 특정 항목이 두 번 사용되면 True를 그렇지 않으면 False를 리턴한다.
- 인자로 사용된 리스트는 수정하지 않는다.
  
  예제:
```
>>> has_duplicates([1, 2, 1, 3])
True
>>> has_duplicates(['hello', 'hi', 'hey'])
False
```
  힌트: 집합(set) 자료형 활용
기본 자료형: 파일에서 다룬 words.txt 파일을 다시 이용한다. words.txt 파일의 내용을 리스트 자료형으로 저장하라. 단, 리스트의 항목은 각 줄에 있는 단어이다.

힌트: for 반복문 활용. 리스트에 단어를 추가할 때 append와 strip 메서드 활용. 정답은 wordlist.py 참고.
위 문제에서 생성된 리스트에 특정 단어가 포함되어 있는지 여부를 확인하는 함수를 리스트 자료형의 in 연산자 활용하여 구현하라.
위 문제에서 구현된 함수를 이진탐색(binary search)을 이용하는 방식으로 수정하여 새로 구현하라. 두 함수의 실행속도의 차이를 비교하라.
이진탐색의 개념과 파이썬 구현은 이진탐색하기를 참조할 수 있다.

힌트: 정답은 inlist.py 참고.
기본 자료형: 파일에서 다룬 words.txt 파일을 다시 이용한다. words.txt 파일의 내용을 사전 자료형으로 저장한 후에, 생성된 사전에 특정 단어가 키로 사용되었는지 여부를 확인하는 함수를 사전 자료형의 in 연산자 활용하여 구현하라.

힌트: words.txt 파일에서 단어를 읽어 들인 후 각각의 단어를 키로 사용한다. 모든 키의 값은 True로 정한다.

앞서 리스트를 활용한 구현 방식과 비교하여 사전 자료형을 이용한 in 연산자의 실행속도가 얼마나 빠른지 확인하라.
양의 정수 n의 팩토리얼 값은 1부터 n까지의 곱셈이다.

n! = n*(n-1)*(n-2)*...*2*1
1. n!을 계산하는 함수 factorial을 아래와 같이 재귀로 구현할 수 있다.
```
def factorial(n):
     if n == 1:
         return 1
     else:
         res = n * factorial(n-1)
         return res
```
  계산가능한 팩토리얼의 한계를 확인하라.
2. 팩토리얼 함수 factorialDynamic를 동적계획을 이용하여 구현한 후에, 계산가능한 팩토리얼의 한계가 달라지는지 확인하라.

기본 자료형: 집합과 사전¶

집합¶

집합 자료형 사용 이유¶

예제¶

예제¶

예제¶

예제¶

사전¶

항목¶

빈 사전 생성¶

항목 추가¶

사전 선언¶

항목의 순서¶

대괄호([]) 연산자¶

'len' 함수¶

'in' 연산자¶

사전 자료형 메서드¶

keys 메서드¶

values 메서드¶

items 메서드¶

예제: 다이빙 기록과 사전 자료형¶

반복문과 사전¶

예제: 카운터¶

동적계획, 리스트, 사전¶

피보나찌 수열¶

동적계획과 리스트¶

동적계획과 사전¶

처리속도: in 연산자¶

연습문제¶

대괄호(`[]`) 연산자¶

`keys` 메서드¶

`values` 메서드¶

`items` 메서드¶

처리속도: `in` 연산자¶